Здравствуйте! Как известно, все газы в той или иной степени отличаются от идеального газа, и при значительном отклонении расчет с помощью уравнения Клапейрона — Менделеева приводит к большим погрешностям. Это обусловлено наличием сил взаимодействия между молекулами реального газа и влиянием их собственного объема. Так например, законы идеальных газов нельзя распространять на рабочие тела, состояния которых не очень удалено от жидкой фазы. Поэтому, к примеру, на водяной пар при давлениях и температурах, обычно применяемых в теплоэнергетике, не распространяется уравнение Клапейрона — Менделева.
Силы, действующие между молекулами, имеют в основном электрическую природу, так как молекулы представляют собой сложную систему двух разноименных зарядов. Поэтому между молекулами существуют как силы отталкивания, обусловленные взаимодействием зарядов одного знака, так и силы притяжения, возникающие из-за наличия зарядов противоположных знаков. Силы отталкивания уменьшаются значительно быстрее, чем силы притяжения, а при сближении молекул они нарастают очень быстро, поэтому в реальном газе не происходит непосредственное соударение молекул, а осуществляется лишь взаимодействие их на расстоянии. На некотором удалении друг от друга между молекулами существуют силы взаимного притяжения.
Отклонение от свойств идеального газа возрастает с увеличением плотности, так как при этом уменьшаются средние расстояния между молекулами.
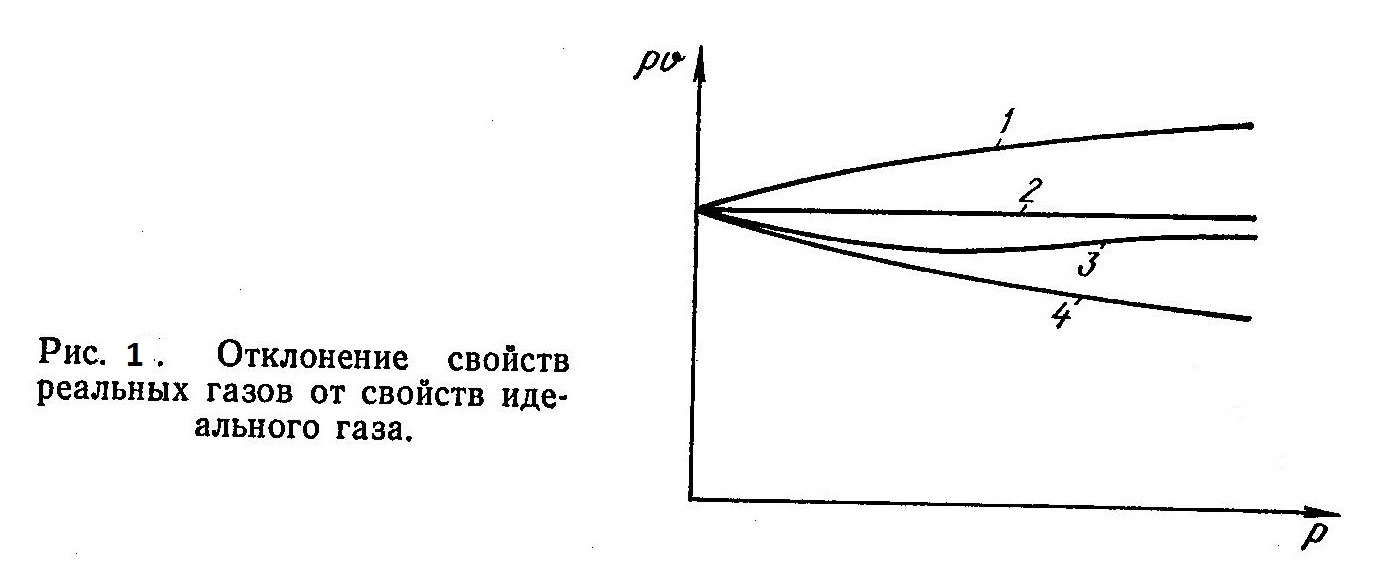
Расхождение свойств реальных газов можно наглядно представить в виде графической зависимости произведения pυ от давления (рис. 1). Согласно уравнению состояния идеального газа , произведение pυ представляет изотерму, которой соответствует горизонтальная прямая 2.
Наличие сил притяжения между молекулами равнозначно некоторому дополнительному давлению, сжимающему газ. С увеличением давления газа уменьшаются расстояния между молекулами и возрастают силы притяжения, а также величина дополнительного давления. В результате удельный объем v реального газа уменьшается сильнее, чем удельный объем идеального газа, и изотерма 4 реального газа на рис. 1 расположена ниже, чем изотерма 2 идеального газа.
Если между молекулами газа преобладают силы отталкивания, то повышение его давления обычно сопровождается уменьшением расстояний между молекулами, что приводит к увеличению сил отталкивания. При этом удельный объем гораздо меньше, чем у идеального газа (изотерма 1), то есть он будет менее сжимаем, чем идеальный.
У большинства реальных газов изотермы имеют характер, аналогичный кривой, изображенной на рисунке как изотерма 3. При невысоких давлениях между молекулами газа существуют силы притяжения и произведение pυ с увеличением давления, как и для изотермы 4, уменьшается. При больших давлениях между молекулами газа преобладают силы отталкивания, что приводит к увеличению произведения pυ с ростом давления.
Одно из первых уравнений состояния реальных газов, которое учитывает их молекулярное взаимодействие и собственный объем молекул, было предложено в 1873 г. нидерландским физиком Ван- дер-Ваальсом
Оно было получено на основе молекулярно-кинетической теории путем введения поправок к уравнению состояния идеального газа . Величина a/υ2 учитывает изменение давления газа, обусловленное силами притяжения между молекулами.
Вследствие взаимного притяжения молекул возникает дополнительное внутреннее давление, сжимающее газ и равное α/υ2. Константа α пропорциональна потенциальной энергии взаимодействующих молекул. Коэффициент b учитывает влияние сил отталкивания. Он измеряется в единицах объема и характеризует уменьшение свободного объема, в котором происходит движение молекул, из-за того что они имеют конечные размеры. Величины α и b зависят от рода газа и могут быть найдены опытным путем.
Экспериментальные исследования показывают, что уравнение Ван-дер-Ваальса (1) является приближенной зависимостью, которая лишь качественно описывает поведение реальных газов и поэтому оно не применяется в технических расчетах. При значительном изменении давления величины α, Ь и R становятся переменными. Наибольшее отклонение от опытных данных наблюдается при высоких давлениях и низких температурах, то есть при высокой плотности газа. Это означает, что в реальных газах существуют более сложные взаимодействия между частицами, не учитываемые уравнением (1).
Общее уравнение состояния реальных газов, полученное методами статистической физики, имеет вид
где βк — коэффициенты, являющиеся функциями температуры.
Для того чтобы достаточно точно описать состояние реальных газов, необходимо значительно увеличивать число слагаемых в правой части уравнения (2). Кроме того, теоретический расчет коэффициентов βк не всегда возможен, так как неизвестен закон взаимодействия молекул данного газа. Поэтому при расчетах термодинамических свойств реальных газов обычно основываются на экспериментальных данных, которые используются для получения эмпирических уравнений и расчетных формул. В литературе приводится большое число различных уравнений состояния, полученных экспериментально и применимых в ограниченном диапазоне изменения параметров состояния газа. Исп.литература: 1) Теплотехника, под общей редакцией И.Н. Сушкина, Москва, «Металлургия», 1973. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,"Вышейшая школа", 1976.


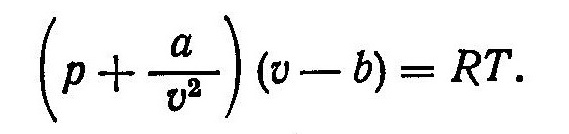
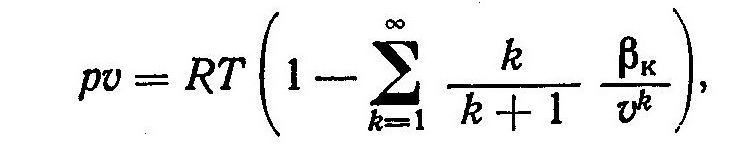
Добавить комментарий