Здравствуйте! В термодинамике все газы, обладающие такими же свойствами, как система невзаимодействующих материальных точек, называются идеальными. Реальные газы при низких давлениях близки к идеальным, ибо в этих условиях силами межмолекулярного воздействия и объемом молекул можно пренебречь. Опыты с реальными газами показывают, что законы, которым подчиняются газы, значительно упрощаются, если не учитывать силы межмолекулярного взаимодействия и собственный объем молекул газа. В соответствии с этим в физику было введено понятие идеального газа, в котором отсутствуют силы взаимодействия между молекулами, а объем их равен нулю.
Реальные газы приближаются к идеальному с уменьшением плотности, когда снижается число молекул в единице объема газа. В обычных условиях законам идеального газа довольно точно подчиняются водород и гелий. Однако технические расчеты и для других газов (кислорода, азота) обычно можно вести по формулам, полученным для идеального газа. Свойства этих газов незначительно отличаются от свойств идеального газа, и такой расчет не приводит к большим погрешностям.
Уравнением состояния идеального газа является уравнение Клапейрона:
Это уравнение установлено экспериментально при изучении связи между параметрами состояния газа. Коэффициент пропорциональности R называется газовой постоянной и измеряется в Дж/(кг* К). Газовая постоянная имеет для каждого газа вполне определенное значение.
Продифференцировав уравнение (1) для случая, когда p = const (изобарный процесс), получим
Согласно этому равенству, газовая постоянная представляет собой работу единицы массы газа pdυ при изменении температуры на одни градус в изобарном процессе.
Уравнение (1) можно записать также для одного киломоля газа, если умножить левую и правую части на молекулярную массу µ:
Величина υµ, выражает объем υ киломоля газа при давлении р и температуре Т. Произведение µR является газовой постоянной для моля газа. Введя обозначение,
получим
Это уравнение состояния для киломоля газа называется уравнением Клапейрона — Менделеева.
Универсальная газовая постоянная Rµ численно равна работе киломоля газа в изобарном процессе при изменении температуры на одни градус. Согласно закону Авогадро, киломоли любых газов, подчиняющихся идеальным газовым законам, в одних и тех же условиях занимают одинаковые объемы. При изменении температуры на один градус в изобарном процессе киломоли этих газов будут изменять объем на одну и ту же величину, т. е. совершать одинаковую работу. Следовательно, постоянная Rµ является универсальной физической величиной, не зависящей от рода газа. Универсальная газовая постоянная Rµ измеряется в Дж,(кмоль*К).
Величину универсальной газовой постоянной Rµ определим, подставив в уравнение (3) объем киломоля газа и значения параметров состояния, соответствующих нормальным условиям (υ= 22,4 нм3 /кмоль, Т = 273 К и р = 1,013-10* Па):
Значение газовой постоянной R для любого газа может быть найдено из выражений (3) и (5). Исп.литература: 1) Теплотехника, под ред. А.П.Баскакова, Москва, Энергоиздат, 1982. 2)Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,"Вышейшая школа", 1976.


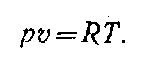
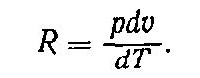
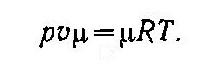
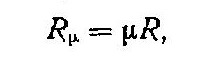
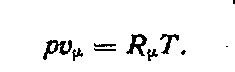
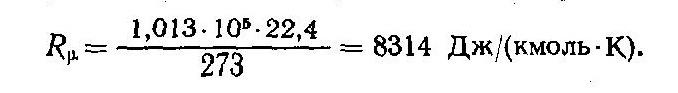
Добавить комментарий