Здравствуйте, друзья! Из дифференциальных уравнений конвективного теплообмена с помощью методов теории подобия находятся следующие числа подобия:
Nu, Re, Ре, Gr, Eu, Pr.
Число Нуссельта Nu, характеризующее интенсивность теплообмена между твердым телом и средой, равно
где α — коэффициент теплоотдачи; l — определяющий (характерный) размер; λс — коэффициент теплопроводности среды.
Обычно при расчете конвективного теплообмена число Nu является искомой величиной, так как в него входит коэффициент теплоотдачи, который неизвестен и подлежит определению, поэтому в уравнениях теплообмена оно всегда выступает в качестве функции. Число Nu представляет собой безразмерную форму коэффициента теплоотдачи.
Несмотря на внешнее сходство с числом Био
число Nu существенно отличается от него. Различие состоит в том, что в число Nu входит коэффициент теплопроводности среды, а в число Bi — коэффициент теплопроводности материала тела. Поэтому число Bi применяется при исследовании процесса распространения теплоты в теле, и условия его взаимодействия с окружающей средой считаются заданными (коэффициент теплоотдачи α известен). По условию задачи обычно известны характерный размер l и коэффициент теплопроводности λ , поэтому Bi является определяющим числом подобия (критерием подобия).
Если учесть, что λ/l — термическая проводимость тела, то число Био можно записать в виде
Отсюда следует, что число Bi характеризует относительную интенсивность теплообмена, то есть интенсивность теплообмена на поверхности тела по сравнению с интенсивностью распространения теплоты внутри тела.
Гидродинамические условия движения потока характеризуются числом Рейнольдса
Это число представляет собой меру отношения инерционной силы к силе внутреннего трения. Оно является важнейшей характеристикой исследуемого процесса и обычно применяется в уравнениях подобия при расчете конвективного теплообмена в условиях вынужденного движения потока.
Безразмерный комплекс
называемый числом Пекле, характеризует перенос теплоты в потоке.
Физические свойства среды через коэффициент кинематической вязкости υ и коэффициент температуропроводности α определяет число Прандтля
Оно может быть получено при делении числа Ре на число Re:
Так как сочетание двух чисел подобия дает третье, то для характеристики явления можно применять любую пару из названных чисел. В большинстве случаев пользуются числами Re и Рг, которые определяют гидродинамические и физические условия, причем число Рг является безразмерным параметром как для вынужденного, так и для свободного движения.
Для каждой среды, если предположить, что ее физические свойства неизменны, число Прандтля имеет вполне определенное численное значение. Для газов число Рг близко к единице, изменяется в небольших пределах 0,67—1,0 и зависит только от атомности газа. Например, для двухатомных газов Рг = 0,72, для жидкостей Рг = 1—2500; большие значения соответствуют очень вязким жидкостям. Число Рг для жидких металлов изменяется в пределах 0,005—0,05. Очень малые значения Рг объясняются высокой теплопроводностью металлов.
Кинематическое подобие при свободном движении жидкости устанавливается числом Грасгофа
где β — коэффициент объемного расширения (для газа β = 1/T); g — ускорение свободного падения; ∆t — разность температур между поверхностью тела и средой.
Число Грасгофа характеризует процесс свободного движения жидкости, обусловленный различием плотности, причем причиной отмеченной неоднородности является температурное поле. Как видно из формулы (1), величина Gr находится в прямой зависимости от температурного напора, коэффициента объемного расширения среды, размера поверхности нагрева по вертикали, ускорения силы тяжести и обратно пропорциональна вязкости, препятствующей развитию свободного движения. Число Gr применяется в уравнениях подобия, используемых для расчета конвективного теплообмена в условиях свободного движения жидкости.
Безразмерный комплекс
где ∆p — перепад давления; ρ — плотность жидкости, называют числом Эйлера.
Это число подобия характеризует соотношение сил давления и сил инерции или, другими словами, сопротивление канала в зависимости от скорости потока и применяется при исследовании гидравлического сопротивления каналов и аппаратов. Искомой величиной является перепад давления ∆р, а масштабом отнесения — ρω^2. В целом число Еu — безразмерная форма неизвестной переменной. Таким образом, число Ей является функцией безразмерных независимых переменных, то есть определяемым числом подобия.
Наиболее важными числами подобия применительно к конвективному теплообмену являются числа Нуссельта Nu, Рейнольдса Re, Грасгофа Gr и Прандтля Рг. Все величины, входящие в числа Re, Gr и Рг, обычно известны по условию задачи, поэтому они представляют собой определяющие числа подобия, являясь одновременно критериями подобия, и входят в обобщенные уравнения в качестве аргументов.
Температура, при которой определяются физические параметры λ, α, υ, входящие в числа подобия, называется определяющей температурой, а характерный размер тела или канала d, I, h — определяющим размером. В зависимости от условий конкретной задачи в качестве определяющей температуры принимается температура среды tc, или температура поверхности тела tп, или средняя температура пограничного слоя tm=0,5t*(tc — tп).
В качестве определяющего размера для трубы принимается диаметр или высота в зависимости от ее ориентации в пространстве; для вертикальной пластины — высота и так далее. При обработке экспериментальных данных в форме уравнения подобия всегда указывается, какая температура и какой размер приняты в качестве определяющих. Исп.литература: 1) Теплотехника, под редакцией А.П. Баскакова, Москва, Энергоиздат, 1982. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,"Вышейшая школа", 1976.


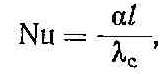
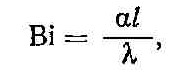
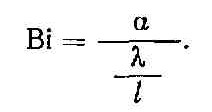
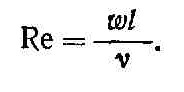
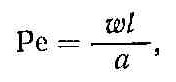
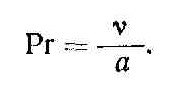
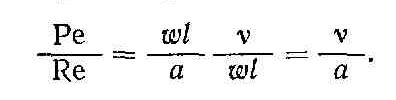
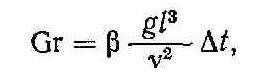
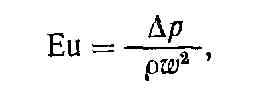
Ого сколько материала выложили, хватит на половину лекции. А если еще задавать вопросы, то как раз всю пару займет.
Мне страшно перед экзаменом. Очень-очень страшно