Здравствуйте, друзья! Эта статью написал для сайта инженера теплоэнергетика teplosniks.ru Александр Лупей. Александр работает главным метрологом ОАО «ТГК-1», г.Санкт Петербург, и в своем деле он настоящий профессионал.
Ежемесячно на любом источнике теплоты, будь то небольшая котельная или крупная ТЭЦ, при подведении итогов работы и расчёте технико-экономических показателей возникает одна и та же проблема несходимости результатов учёта потребляемой холодной воды и отпускаемой в тепловые сети подпиточной воды. Проблема водных (а, следовательно, и тепловых) небалансов особенно заметна на крупных источниках теплоты, имеющих несколько отходящих тепломагистралей.
Действующие ныне нормативные документы не содержат каких-либо указаний по разрешению данного вопроса. Но, коль скоро в отчётах, составляемых на источниках теплоты, небаланса быть не должно, то и решается эта проблема различными способами, многие из которых вряд ли можно отнести к числу логичных или сколь-нибудь обоснованных.
Если на источнике теплоты все необходимые измерения правильно организованы, то можно утверждать, что единственной причиной небалансов являются систематические погрешности применяемых средств измерений (СИ). Поэтому представляется наиболее правильным и обоснованным осуществлять сведение водных балансов с учётом нормированных метрологических характеристик всех СИ, показания которых в той или иной мере могут влиять на величину небаланса.
Сегодня, получив свидетельство о поверке того или иного СИ, владельцу СИ ничего не известно ни о размере, ни о знаке систематической погрешности СИ; известно лишь то, что, например, данный преобразователь или вторичный прибор «имеет приведенную погрешность не более 1%», или «годен к применению по классу С», или «годен с относительной погрешностью не более ±2%» и т.п. Именно это обстоятельство не позволяет определить конкретных виновников имеющихся небалансов для того, чтобы внести в их показания необходимые поправки в соответствии с величиной и знаком выявленной при поверке систематической погрешности, тем самым существенно улучшив сходимость результатов измерений.
Единственное, что можно предпринять в данной ситуации — это рассчитать максимально возможную величину небаланса на основе измеренных значений массы воды во всех точках учета и пределов допускаемой погрешности каждого СИ, полагая при этом, что систематическая погрешность всех СИ равна предельно допускаемому значению, указанному в паспорте прибора, а знак этой погрешности способствует увеличению небаланса.
Сопоставив фактически имеющийся небаланс с максимально возможным в данных условиях, можно сделать обобщенный вывод о качестве выполненных измерений: если фактический небаланс приближается к максимально возможному, или превышает предельно допустимое значение, то это наверняка свидетельствует о неисправности одного или нескольких приборов учета; в этой ситуации сведение баланса с учётом нормированных метрологических характеристик недопустимо.
Если же на рассматриваемом интервале времени (сутки, декада, месяц) имеющийся фактический небаланс сравнительно невелик по отношению к предельно допустимому небалансу, то с некоторой уверенностью можно предположить, что все измерения выполнены достаточно корректно (по крайней мере, можно утверждать, что средневзвешенная систематическая погрешность результатов измерений находится в «разумных» пределах). В этом случае для устранения имеющегося небаланса представляется оправданным и, пожалуй, единственно возможным выполнить принудительную корректировку полученных результатов измерений с обязательным соблюдением следующих правил:
— корректировке подлежат только те результаты измерений, которые могут служить причиной небаланса;
— знак вводимой поправки должен быть таким, чтобы её применение способствовало уменьшению имеющихся расхождений;
— относительная величина поправок должна быть прямо пропорциональна пределам допускаемых относительных погрешностей измерений соответствующих величин;
— коэффициент пропорциональности должен быть одинаков для всех приборов учёта и определяться отношением фактического небаланса к его предельно допустимому значению.
Рассмотрим на конкретном примере порядок применения вышеуказанных принципов при решении задачи устранения водного небаланса, вызванного погрешностями СИ, применяемых в узлах учёта потребляемой холодной воды и отпускаемой тепловой энергии.
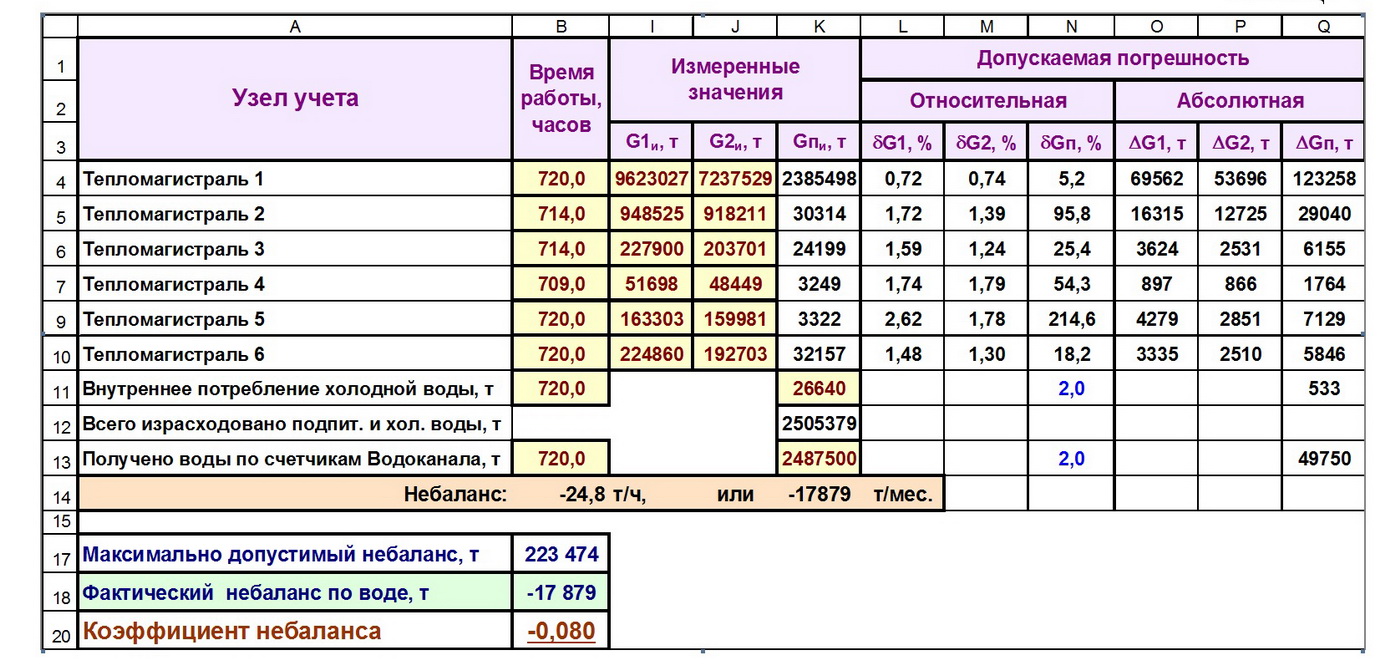
В таблице 1 приведены результаты измерений, полученные на источнике теплоты в ноябре месяце. Из таблицы видно, что в данном месяце на источнике имел место отрицательный водный небаланс, равный -17879 т (ячейка К14), или в среднем -24,8 т/ч, т.к. по показаниям приборов учета потребление воды составило 2487500 т (ячейка К13), а израсходовано на подпитку тепловых сетей и хозяйственные нужды 2505379 т (ячейка К12).
Таблица 1
Ясно, что около 18000 тонн воды не могли взяться ниоткуда, и этот небаланс в результатах учёта отпуска и потребления вызван исключительно погрешностью измерений, выполненных в узлах учёта холодной и горячей воды. Очевидно, что в данной ситуации мы не можем с уверенностью определить конкретного «виновника» возникшего небаланса, но нам известно то, что погрешность измерений каждого измерительного канала не превышает допускаемых значений (по крайней мере, по результатам последних поверок все СИ признаны годными для эксплуатации).
Расчетные значения пределов допускаемых относительных погрешностей измерения расхода в подающих и обратных трубопроводах отходящих от источника тепломагистралей указаны в ячейках L4-M10, относительная погрешность водосчётчиков, установленных на трубопроводах приобретаемой холодной воды и трубопроводах собственных нужд, по данным последней поверки не превышает 2% (ячейки N13 и N11).
Следует обратить внимание на допускаемую относительную погрешность измерения разности расходов воды (подпитки Gп) в тепломагистралях: если сами расходы G1 и G2 здесь измеряются с погрешностью 0,72-2,62%, то допускаемая погрешность измерения разности расходов во много раз больше (для магистрали 1 — в 7,1 раза, для магистрали 5 — в 97,5 раза).
На основании допускаемых относительных погрешностей рассчитаем пределы допускаемых абсолютных погрешностей измерения массы воды в подающих (ΔG1) и обратных (ΔG2) трубопроводах тепломагистралей (ячейки О4-Р10), а также погрешности счетчиков внутреннего потребления холодной воды (ячейка Q11) и счётчиков городской воды (ячейка Q13). Просуммировав значения ячеек Q4-Q13, получим расчётную величину максимально допустимого небаланса, равного ±223474 т за месяц (ячейка В17).
Теперь можно рассчитать средний коэффициент небаланса Кнб (ячейка В20), равный отношению фактического небаланса к его максимально возможному при имеющихся результатах измерений:
Кнб = -17879/223474= -0,080.
Таким образом, результаты измерений свидетельствуют о том, что имеющийся небаланс составляет всего 8% от максимально допускаемого значения, возможного в случае, когда действительные погрешности всех СИ достигнут своих предельно допускаемых значений.
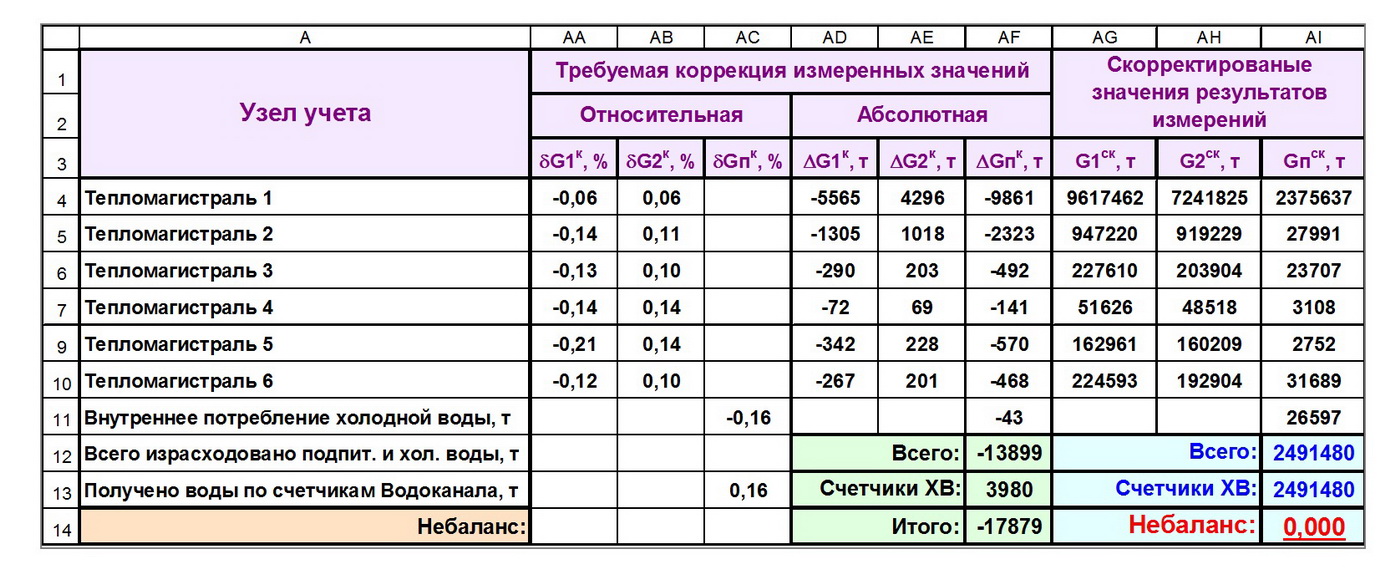
Зная величину и знак среднего коэффициента небаланса, можно рассчитать величину требуемой коррекции всех измеренных значений как в относительном (ячейки АА4-АВ10), так и в абсолютном (ячейки AD4-AF11 и AF13) виде. Видно, что для достижения идеального водного баланса результаты измерений необходимо скорректировать следующим образом:
— измеренные значения масс воды в подающих трубопроводах тепломагистралей уменьшить на -0,06 ÷ -0,21% (ячейки АА4-АА10);
— показания расходомеров воды, установленных в обратных трубопроводах, увеличить на +0,06 ÷ +0,14% (ячейки АВ4-АВ10);
— показания счётчиков внутреннего потребления холодной воды уменьшить на -0,16% (-43 т);
— результаты учёта холодной воды, полученной источником теплоты, увеличить на плюс 0,16% (+3980 т).
После такой корректировки всех результатов измерений количество полученной источником воды (2491480 т, ячейка AI13) будет в точности равно количеству воды, израсходованной на подпитку внешних тепломагистралей и внутреннее потребление (ячейка AI12), а значение небаланса будет равно нулю (ячейка AI14).Сегодня не существует официальных рекомендаций как по расчёту максимально допускаемой величины небаланса GНБ = Gп — ∑(G1i-G2i) между подпиткой Gп, и суммой разностей показаний расходомеров, установленных на подающих (G1i) и обратных (G2i) трубопроводах отходящих магистралей, так и по способам корректировки этого небаланса обоснованными методами. В то же время в некоторых публикациях предлагается распределять небаланс подпиточной воды пропорционально измеренным разностям масс теплоносителя на каждой из отходящих тепломагистралей, т.е. в соответствии с формулой (1):
В формуле (1) приняты следующие обозначения: N – число магистралей, отходящих от источника; Gпi – исправленная (скорректированная) масса подпиточной воды в i-й магистрали; Gп – масса подпиточной воды, измеренная расходомером (расходомерами) подпитки; (G1i-G2i) – масса подпиточной воды i-й магистрали, измеренная как разность показаний сетевых расходомеров G1 и G2.
Анализ формулы (1) показывает, что её применение на практике нежелательно, т.к. эта формула предполагает распределение имеющегося небаланса только пропорционально разности показаний сетевых расходомеров и никак не учитывает точность выполненных измерений массы подпиточной воды Gп и суммы разностей масс G1i-G2i.
Кроме того, формула (1) не учитывает точность измерений, выполненных подпиточным расходомером (или расходомерами, если их несколько), т.е. при таком подходе подпиточные расходомеры Gп считаются идеально точными. Но на практике показания любого расходомера всегда в той или иной мере ошибочны, и подпиточные расходомеры, несомненно, вносят свой вклад в водные небалансы на любом источнике теплоты. Но формула (1) предполагает, что весь имеющийся небаланс следует относить на измеренные разности масс магистральных расходомеров (G1i — G2i), а погрешность расходомера подпитки при этом считается нулевой и его показания – абсолютно истинными.
Очевидно, что такой подход вряд ли допустим при ведении коммерческого учёта, ибо расходомер (расходомеры) подпитки, как и сетевые расходомеры, измеряет расход (массу) с некоторой погрешностью, и эта фактическая погрешность тоже является источником небаланса наряду с погрешностями сетевых расходомеров.
Существует и третья причина, по которой применение формулы (1) «в чистом виде» невозможно. Суть этой проблемы заключается в следующем.
Предположим, что по итогам работы за сутки имеющийся водный небаланс распределён между магистралями по формуле (1). Пусть, например, на одной из отходящих магистралей показания расходомеров (измеренные значения) составили: G1и = 1000 т, G2и = 900 т, G1и — G2и = 1000 — 900 = 100 т. Предположим, что имеется положительный небаланс (т.е. подпитка Gп больше суммы разностей масс на магистралях), который мы распределяем по формуле (1). Пусть в соответствии с формулой (1) на эту магистраль пришлась доля небаланса подпиточной воды, равная 50 т. Следовательно, мы прибавим к имеющимся (измеренным) 100 т дополнительные «балансовые» 50 т, и в итоге получим, что подпитка этой магистрали равна G1ф-G2ф = 100 + 50 = 150 т.
Точно так же мы поступим и с прочими магистралями, и сумма разностей расходов на магистралях после такой «балансировки» по формуле (1) будет в точности равна показаниям расходомера подпитки Gп. И задача сведения баланса по подпиточной воде как бы решена.
Но тут возникает проблема: разности масс по каждой магистрали скорректированы, водный баланс по подпиточной воде обеспечен, но показания расходомеров G1i и G2i остались неизменными. Хотя очевидно, что, исправив разность масс (вместо измеренных 100 т мы получили «фактические» 150 т), необходимо исправить и показания самих расходомеров G1 и G2. Если этого не сделать, то неизбежно возникает разбаланс результатов учёта уже на каждой магистрали: в отчёте о теплоотпуске будет указано, что показания расходомеров на магистрали №1 G1 = 1000 т, G2 = 900 т, но одновременно их разность будет равна 150 т.
Следовательно, принудительно прибавив к имеющимся 100 тоннам разности масс «балансовые» 50 тонн, необходимо скорректировать G1 и G2 таким образом, чтобы на магистрали тоже выполнялся баланс масс G1ф — G2ф = 150 т. И уже после корректировки значений G1 и G2 необходимо пересчитать (с учетом исправленных масс) и тепловую энергию, отпущенную по магистрали. Иначе получится, что тепловую энергию, отпущенную по магистрали, теплосчётчик рассчитал для измеренных значений G1и, G2и и (G1и — G2и), при сведении баланса по подпитке получены другие значения масс G1ф и G2ф, но тепловая энергия при этом осталась прежней.
Поэтому, заменив измеренные 100 т подпитки магистрали на требуемые для обеспечения водного баланса 150 т, необходимо эти «лишние» 50 т распределить между G1 и G2 так, чтобы выполнялось условие G1ф — G2ф = 150 т. И здесь возникает принципиальный вопрос о критериях распределения этих фактически не измеренных 50-и тонн между показаниями расходомеров G1 и G2. В этой связи представляется наиболее корректным принцип распределения водного (а затем и теплового) небаланса не пропорционально измеренным разностям расходов (G1i — G2i), а пропорционально точности выполненных измерений.
Покажем на конкретном упрощённом примере, что формула (1) при сведении баланса приводит к весьма некорректному результату, а вот метрологический подход к устранению небаланса вполне применим на практике.
Пусть имеется некий источник теплоты с двумя двухтрубными магистралями, имеющими общий обратный коллектор. На подающих и обратных трубопроводах этих магистралей установлены расходомеры G1 и G2. Для подпитки этих магистралей имеется один общий подпиточный трубопровод с расходомером Gп.
Так же для упрощения рассуждений и расчётов условимся, что горячая вода после расходомера Gп не отбирается на хознужды ТЭЦ, а расходуется исключительно на подпитку этих двух магистралей. Так же будем считать, что каких-либо потерь воды за расходомером Gп нет. Следовательно, при сделанных допущениях и нулевой ошибке измерений всех пяти расходомеров должно выполняться равенство Gп = (G11-G21) + (G12-G22).
Пусть по итогам работы (например, за сутки) измеренные значения суточных масс составили: G11 = 2000 т; G21 = 1500 т; Gп1 = 2000 – 1500 = 500 т; G12 = 50000 т; G22 = 49500 т; Gп2 = 50000 – 49500 = 500 т; Gп = 1500 т.
Видно, что подпиточный расходомер Gп измерил 1500 т за сутки, а сумма разностей показаний магистральных расходомеров равна 1000 т. Положительный небаланс равен: GНБ = 1500—1000 = 500 т за сутки.
Коль скоро в данном примере измеренные значения подпитки магистралей равны (по 500 т в каждой), то по формуле (1) находим, что имеющийся небаланс в 500 т распределяется между магистралями поровну, в пропорции 1:1, т.е. на каждую магистраль приходится по 250 т имеющегося небаланса.
В результате сведения баланса получим, что: G11 = 2000 т; G21 = 1500 т; Gп1 = 2000 – 1500 = 750 т; G12 = 50000 т; G22 = 49500 т; Gп2 = 50000 – 49500 = 750 т; Gп = 1500 т.
После такого распределения небаланса видно, что:
— показания расходомеров G1i и G2i остались прежними, что привело к неравенству выражений Gпi = G1i — G2i на обеих магистралях;
— показания подпиточного расходомера (Gп) не подверглись корректировке, т.е. предполагается, что погрешность подпиточного расходомера равна нулю;
— распределение небаланса между двумя магистралями выполнено в равной пропорции 1:1 без учёта точности выполненных измерений разностей масс G1i — G2i.
Очевидно, что такой подход к сведению водного баланса не несёт в себе ни технологической, ни метрологической обоснованности, поэтому не может быть рекомендован к применению на практике. Представляется, что единственно возможным критерием сведения водного баланса на источнике теплоты должен служить критерий точности выполненных измерений, в соответствии с которым имеющийся небаланс распределяется пропорционально допускаемым абсолютным погрешностям всех (в том числе и подпиточных) расходомеров, чьи показания могут влиять на размер небаланса.
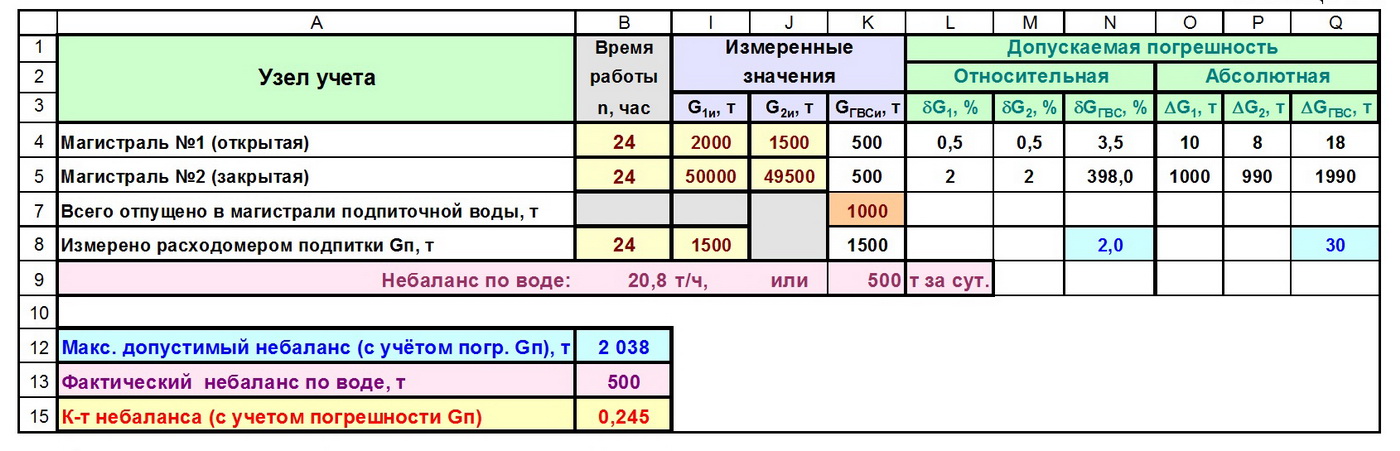
В таблице 1 показан пример сведения водного баланса для ранее рассмотренного случая наличия на источнике одного расходомера подпитки и двух отходящих магистралей. В этом примере условно принято, что расходомеры G11 и G21, установленные на магистрали №1, имеют допускаемую относительную погрешность ±0,5%, расходомеры G12 и G22, установленные на магистрали №2, и расходомер подпитки Gп имеют допускаемую относительную погрешность, равную ±2%.
Имея суточные показания всех расходомеров и зная допускаемую относительную погрешность каждого их них, можно рассчитать допускаемую абсолютную погрешность каждого из пяти расходомеров, а также допускаемую абсолютную погрешность разности показаний магистральных расходомеров (столбцы O, P, Q в табл. 1-1).
Здесь мы должны обратить внимание на следующее принципиальное обстоятельство. Не смотря на то, что измеренные разности масс на каждой из магистралей одинаковы (по 500 т за сутки), допускаемая абсолютная погрешность измерения этих разностей весьма различна: для магистрали №1 допускаемая абсолютная погрешность равна ±18 т, а для магистрали №2 — ±1990 т, что в 111 раз больше, чем для магистрали №1.
Именно столь значительная неравноточность измеренных разностей масс на двух магистралях не позволяет распределять между ними небаланс в равной пропорции 1:1. Введем понятие «коэффициент небаланса КНБ», который с вероятностью Р = 1 характеризует некий общий уровень неточности выполненных измерений и определяется как отношение фактического небаланса GНБф к максимально возможному небалансу GНБmax, определённому по метрологическим допускам расходомеров для Р = 1.
Очевидно, что при неравноточных измерениях имеющийся небаланс следует распределять пропорционально допускаемой абсолютной погрешности выполненных измерений с учётом имеющего место коэффициента небаланса КНБ.
Из таблицы 1-1 видно, что в рассматриваемом примере GНБф = 1500 – 1000 = 500 т, GНБmax = 18 + 1990 + 30 = 2038 т, поэтому КНБ = 500/2038 = 0,245. Иными словами, в данном примере фактически имеющийся небаланс по подпиточной воде составил только ¼ часть того небаланса, который мог бы иметь место в том случае, если бы фактические погрешности применяемых расходомеров достигли предельно допускаемых значений. Такую несходимость результатов измерений (при КНБ = 0,245) можно считать метрологически благополучной, поскольку КНБ более чем четырёхкратно меньше единицы.
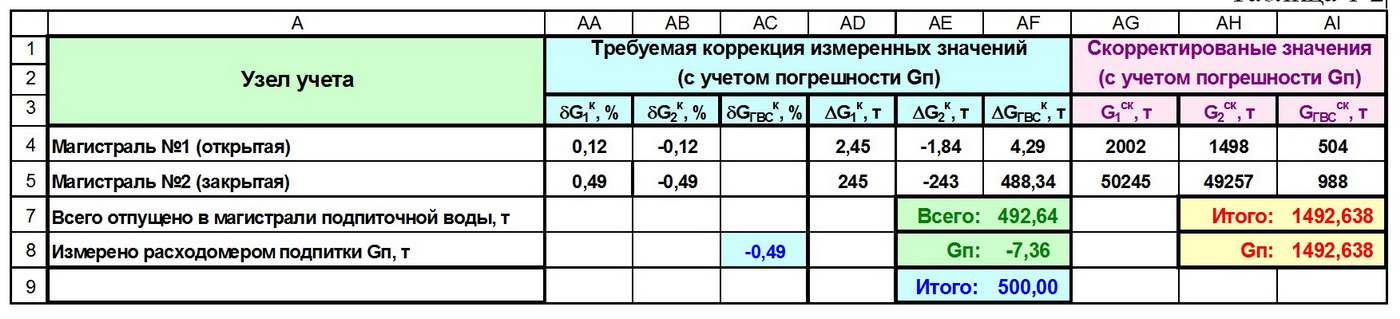
Теперь, зная значение КНБ, можно рассчитать величину относительных и абсолютных поправок к измеренным значениям суточных масс, после чего можно найти скорректированные значения суточных масс, измеренных всеми пятью расходомерами, применяемыми в данной измерительной системе (таблица 1-2).
В результате внесения поправок к показаниям всех расходомеров, пропорциональных КНБ и допускаемой погрешности, небаланс стал равным нулю [Gп = ∑(G1i-G2i)] = 1492,638 т, при этом определены новые (скорректированные) значения показаний всех пяти расходомеров, чьи показания могли служить источником небаланса.
В результате такого метрологического подхода к распределению небаланса каждый из его «участников» получил свою метрологически обоснованную долю небаланса: к измеренной разности масс на магистрали №1 добавлено только 4 т небаланса (здесь измерения разности масс сравнительно точны, δGГВС = ±3,5%), подпитка магистрали №2 увеличена на 488 т (на этой магистрали разность масс измеряется крайне неточно, δGГВС = ±398%), а показания расходомера подпитки уменьшены на 7 т (δGп = ±2%). Таким образом, применяя метрологический подход к проблеме устранения небаланса, мы устраняем все недостатки формулы (1), отмеченные ранее, и тем самым обеспечиваем возможность последующей корректировки результатов учёта тепловой энергии, отпускаемой по магистралям.
Необходимо отметить, что при применении такого метрологического подхода в устранении водного небаланса должны участвовать показания расходомеров собственных и хозяйственных нужд, т.к. и эти расходомеры, измеряющие массу теплоносителя с нормированной погрешностью, тоже должны брать на себя соответствующую долю небаланса. Если на источнике теплоты такие расходомеры не установлены, то при сведении баланса следует применять расчётное значение внутреннего потребления горячей воды, но с обязательным указанием допускаемых отклонений, например: суточное расчётное потребление горячей воды на хоз. нужды Gхн = 10 т ± 1 т. Тогда при сведении баланса и на этот расчётный объём Gхн будет отнесена соответствующая доля небаланса, пропорциональная допуску (±1 т) и коэффициенту небаланса КНБ.
Так же следует иметь ввиду и то, что для каждой измерительной системы (для каждого источника теплоты) всегда существует конкретное граничное значение КНБгр < 1, при превышении которого метрологический подход к сведению баланса применять недопустимо, ибо при КНБ > КНБгр высока вероятность (более 0,95) метрологической неисправности одного или нескольких расходомеров, установленных на магистралях и (или) подпиточных трубопроводах.
Очевидно, что при КНБ > КНБгр ситуацию следует считать метрологически неблагополучной и необходимо принимать меры по выявлению неисправных расходомеров, находящихся в эксплуатации, и отправке их в ремонт.
Практика применения такого метода корректировки водных небалансов на источниках теплоты показывает, что граничное значение КНБгр обычно находится в пределах от 0,35 до 0,45. Следовательно, до тех пор, пока фактический КНБ < 0,35÷0,45, можно устранять небаланс предложенным выше способом. Однако при больших значениях КНБ вероятность того, что на источнике теплоты имеются неисправные расходомеры (подпиточные или сетевые), весьма высока.
Лупей Александр Григорьевич,
главный метролог ОАО «ТГК-1», г.Санкт-Петербург


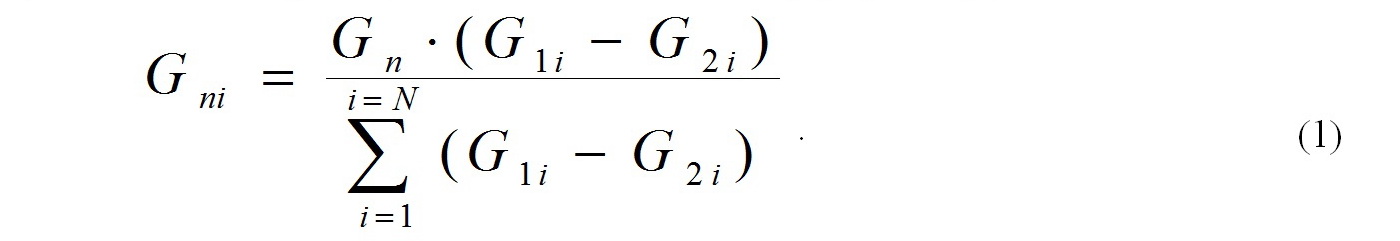
Доброе время суток! Очень заинтересновала меня данная статья, т.к. замучил небаланс на узлах учета тепловой энергии. Применим ли этот метод для моей ситуации? Как получить расчетное значение пределов допускаемой относительной погрешности измерения расхода? Интересно,в допуске ли у меня приборы считают,аль нет... За ответ Большущее спасибо.
Несомненно: если небаланс масс в узле учета тепла обусловлен фактическими погрешностями применяемых расходомеров (доказано, что физические утечка или подпитка отсутствуют), то устранение этого небаланса необходимо выполнять метрологическими методами.
Разумеется, привлекать метрологию к сведению водного (а затем и теплового) баланса в узле учета можно только тогда, когда наблюдаемый небаланс не превышает метрологического допуска. В противном случае мы будем «балансировать» показания неисправных расходомеров, эксплуатация которых в сфере Государственного регулирования обеспечения единства измерений запрещена (ГРОЕИ – к этой сфере регулирования относится и коммерческий учет).
Самый простой случай – это небаланс масс М1 (масса в подающем трубопроводе) и М2 (масса в обратном трубопроводе) в закрытой системе теплоснабжения.
Из-за неравенства фактических погрешностей измерения масс М1 и М2 по размеру и/или по знаку результаты этих измерений всегда не совпадают – по данным архивов теплосчетчика или М1 > М2 (измерена положительная «утечка»), или М1 < М2 (получается отрицательная «утечка», т.е. подпитка).
Допускаемое относительное расхождение масс М1 и М2 рассчитывают по формуле
dM12доп = (dM1доп^2 + dM2доп^2)^0,5 (1),
где dM1доп и dM2доп – допускаемые относительные погрешности измерения масс М1 и М2 соответственно.
Если, например, в закрытой системе применяются два расходомера, у которых dM1доп = dM2доп = +/-1 %, то по формуле (1) находим, что dM12доп = +/-1,4 %.
Следовательно, эта пара расходомеров может эксплуатироваться до тех пор, пока их показания расходятся менее чем на +/-1,4 % от полусуммы ПС = (М1 + М2)/2. В таком случае желательно устранить измеренную «утечку» или «подпитку» принудительным распределением имеющегося небаланса масс между двумя расходомерами в равной пропорции, т.к. измерения масс М1 и М2 являются равноточными.
Если же фактическое расхождение масс М1 и М2 превышает +/-1,4 %, то вероятность исправного состояния одного или обоих расходомеров близка к нулю. Тут уже потребуется метрологическое обслуживание расходомеров – чистка, промывка, регулировка с применением эталонного (высокоточного) расходомера (если чистка и промывка не дали нужного результата), внеочередная поверка.
Большое спасибо за потраченное на меня время. У меня вытекает следующий вопрос: Применимы ли вышеизложенные формулы для Объемов?
Нет, не применимы.
Расхождение измеренных объемов V1 и V2 зависит как от расхождения факт. погрешностей расходомеров, так и от температур воды Т1 и Т2 и их разности DT12 = Т1 – Т2. При этом действует правило: чем больше перепад температур на тепловом вводе, тем больше абсолютное (в м3) и относительное (в процентах от V1, или от V2, или от полусуммы (V1 + V2)/2) расхождения измеренных объемов.
Причина интенсивной зависимости разности объемов от разности температур – в зависимости плотности воды от температуры: чем выше температура воды, тем меньше её плотность и тем больший объем занимает вода при неизменной массе.
На практике всегда выполняется условие Т1 > Т2, поэтому разность объемов DV12 = V1 – V2 всегда больше разности масс DM12 = М1 — М2. Т.е. объемная «утечка» (абсолютная и относительная) всегда больше утечки массовой.
Возьмем какой-нибудь архив теплосчетчика из закрытой системы, в котором архивируются и массы М1 и М2, и объемы V1 и V2.
По данным архива имеем: Т1 = 94 °С, Т2 = 61 °С, DT12 = 33 °C.
Относительное расхождение масс dM12 = ((M1 – M2)/ПСm)*100 % = +0,5 %, что вполне приемлемо для расходомеров с допускаемой погрешностью +/-1 %.
При этом относительное расхождение объемов dV12 = ((V1 – V2)/ПСv)*100 % = +2,6 %, т.е. в 5 раз больше, чем отн. расхождение масс dM12. И уже можно принимать неверное решение о неисправности данной пары расходомеров. На самом деле эта пара расходомеров имеет рассогласование всего в +0,5 % при допуске +/-1,4 %.
Вот здесь: http://forum.primteplo.ru/viewtopic.php?f=5&t=273&start=180">forum.primteplo.ru/viewto...&t=273&start=180 имеется записка «про кубы и тонны», в которой на конкретных примерах показана степень искажения результатов учета при подмене масс М1 и М2 объемами V1 и V2.
Спасибо вам большое. Даже самые «близкие» коллеги не могут объяснить элементарное.
На РТС работает один вывод. G1= 4799т/час; G2=4559т/час; Gпод= 11т/час Разница составляет 240т/час. — 5%. С какой погрешностью работают приборы.
Приборы электромагнитные ВИС.Т кл.т.1%. Из Вашего расчета я поняла , что 94т/час должна быть разница между приборами. 94т/час :2 =46т/час , должна прибавить к каждому показанию вывода.G1=4799+46=4845т/час; G2=4559+46=4605/час
4845—4605=240т/час И на какой документ можно ссылаться. Заранее спасибо.!
Уважаемый Александр Григорьевич!
Я, Богданов Александр Борисович, проработал в большой энергетике 49 лет, и в настоящее время являюсь неофициальным
«Аналитиком теплофикации» теплоэнергетических систем городов, крупных ТЭЦ, ГРЭС, котельных и тепловых сетей. exergy.narod.ru
В настоящее время, меня пригласили в качестве аналитика в МП г. Омска «Тепловая Компания», для выявления причин сверхнормативных
потерь тепловой энергии и особенно утечек подпиточной воды в тепловых сетях г. Омска.
В период 1995—2000г я уже сталкивался с причиной метрологической недостоверности систем измерения «больших и малых расходов водопотребления» 18) «ложных стоков» от недостоверности коммерческого учета «больших и малых расходов» водопотребления и водоотведения. exergy.narod.ru/er2010-01.pdf
В интернете я нашел Вашу статью «О проблеме водных небалансов на источниках теплоты и способов её преодоления». Новости теплоснабжения №10 2016г Сильная статья! Но чувствую что это только малая часть ваших материалов, что принял журнал к печати.
Одной из основных причин проблем огромных погрешностей в анализе балансов воды и особенно в достоверности анализа и статистической отчетности водопотребления, топливо-использования ( удельного расхода условного топлива УРУТ) является отсутствие «Методов сведения балансов и калибровки измерительных приборов учета» сложных теплоэнергетических систем состоящей из десятков отдельных измерительных систем.
К сожалению, мало кто может позволить себе понять и принять управляющее решение по корректировке существующих нормативов.
Александр Григорьевич!
Пришлите мне пожалуйста какие либо ваши статьи, выводы дополнения, что бы я мог их проанализировать и сослаться на них в своих выводах!
exergy.narod.ru/cok2022-08.pdf
-------------------------------------------
С уважением,
аналитик теплофикации России Богданов А.Б.
Омск 8 923 681 53 33 личный сайт «Эксергия Богданов» exergy.narod.ru